Elecciones a líder del proyecto Debian 2020

Línea temporal

Periodo de nominación: Domingo 8 de marzo de 2020 00:00:00 UTC Sábado 14 de marzo de 2020 23:59:59 UTC
Periodo de campaña: Domingo 15 de marzo de 2020 00:00:00 UTC Sábado 4 de abril de 2020 23:59:59 UTC
Periodo de votación: Domingo 5 de abril de 2020 00:00:00 UTC Sábado 18 de abril de 2020 23:59:59 UTC

Tenga en cuenta que el nuevo mandato para el o la líder del proyecto comenzará el 21 de abril de 2020.

Nominaciones

  1. Jonathan Carter [jcc@debian.org] [correo de nominación] [programa]
  2. Sruthi Chandran [srud@debian.org] [correo de nominación] [programa]
  3. Brian Gupta [bgupta@debian.org] [correo de nominación] [programa]

La papeleta, cuando esté lista, se puede solicitar mediante el envío de un correo electrónico firmado a ballot@vote.debian.org con asunto leader2020.

Datos y estadísticas

Este año, como siempre, se obtendrán estadísticas de forma periódica durante el periodo de votación sobre las papeletas recibidas y sobre los acuses de recibo enviados. Además, la lista de votantes quedará registrada. También estará disponible para su consulta la hoja del escrutinio. Recuerde que en la elección del o la líder del proyecto el voto es secreto, por lo que la hoja de escrutinio no contendrá el nombre del o la votante, sino un HMAC que permitirá a cada votante comprobar que su voto está en la lista. Hay una clave generada para cada elector y electora, que se le envía junto con el acuse de recibo del voto.

Quórum

Con la lista actual del censo de desarrolladores y desarrolladoras, tenemos: 

 Número actual de desarrolladores = 1011
 Q ( raíz cuadrada (num. desarrolladores) / 2 ) = 15,8981130955846
 K min(5, Q )           = 5
 Quorum  (3 x Q )       = 47,6943392867539

Quorum

Mayoría necesaria

El candidato o candidata necesita mayoría simple para ser elegible.

Mayoría

Resultado

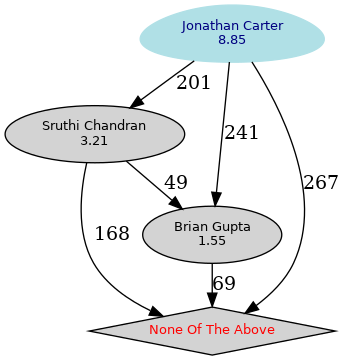
Representación gráfica de los resultados

En el gráfico anterior los nodos rosa indican que esa opción no ha superado la mayoría y la azul es la opción ganadora. El octógono se utiliza para las opciones que no han batido a la opción por omisión.

En la tabla siguiente, escrutinio[fila x][columna y] representa el número de votos en los que se prefiere la opción x sobre la opción y. Una explicación más detallada de la matriz de duelos puede ayudar a entender la tabla. Para entender el método Condorcet, la entrada de la Wikipedia es bastante informativa.

Matriz de duelos
 Opción
  1 2 3 4
Opción 1   258 281 301
Opción 2 57   163 244
Opción 3 40 114   194
Opción 4 34 76 125  

Mirando a la fila 2, columna 1, en 57 votos
se prefirió a Sruthi Chandran sobre Jonathan Carter.

Mirando a la fila 1, columna 2, en 258 votos
se prefirió a Jonathan Carter sobre Sruthi Chandran.

Enfrentamientos por parejas

El conjunto de Schwartz contiene

Los ganadores

Debian utiliza el método Condorcet en las votaciones. Esquemáticamente, el método Condorcets se puede enunciar de la siguiente manera:
Considérense todos los posibles enfrentamientos entre pares de candidatos. El ganador Condorcet, si es que hay alguno, es el candidato que puede vencer a todos los demás en dichos enfrentamientos entre pares. El problema es que, en votaciones complejas, puede haber un resultado circular en el que A vence a B, B vence a C y C vence a A. Las distintas variaciones de Condorcet usan diferentes maneras de resolver el empate. Consulte Cloneproof Schwartz Sequential Dropping («el método Schulze») para más detalles. La variación de Debian está articulada en la constitución, en concreto, en A.6.

El secretario del proyecto Debian